対象学年:5年生以上
子どもたちにとって計算練習とはどのような時間でしょうか。プリントにひたすら取り組む時間となりがちですよね。「計算練習」と聞くとみなさんのクラスの子どもたちはどのような反応をされますか。
「えぇ~やだぁ。」「めんどくさい~。」
そんな声が多いのではないでしょうか。「学ぶこと」「賢くなること」は本来楽しいことであり「できるようになること」は喜びを感じることであるはずなのに、このような反応が出てしまうのは悲しいですね。そんな単調になりがちな時間にちょっとスパイスをプラスできれば計算練習の時間にも「笑顔」が生まれるのではないでしょうか。
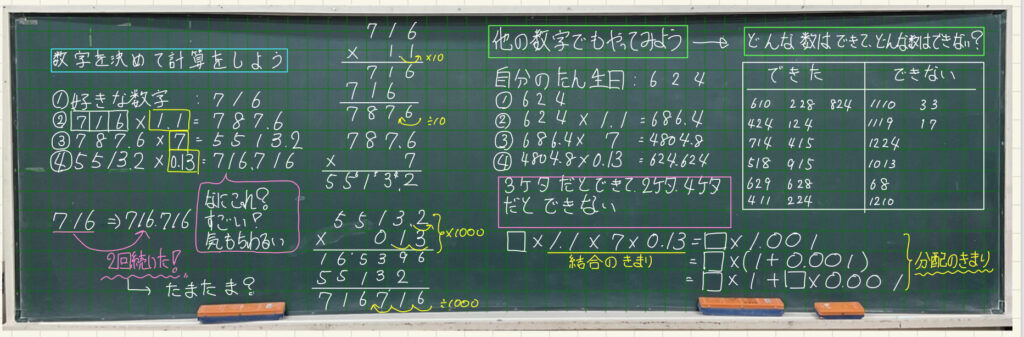
数字を決めて計算をしよう
「今日は計算練習をするよ。」と授業をスタートします。
まずは好きな3けたの数字を選ぶようにつたえます。
どんな数字でもOKです。
ここでは716としておきましょう。
1の数字に1.1をかける
716××1.1ですので787.6になります。
ここでは特に何も起こりません。シンプルに計算練習です。
2の答えに7をかける
787.6×7=5513.2ですね。
3の答えに0.13をかける
5513.2×0.13は…
このあたりで子どもたちから
Cえ?
Cうわぁ!すごい!
Cえ、奇跡?
というような声が出始めます。
中にはそんな友達の反応を見て「???」という子もいます。きっと計算ミスをしたのでしょう。
そこで、
Tえ?なんかざわざわしているけど何かあった?
と、あくまでさらっと聞いてみるとよいですね。すると、
C同じ数が続いたよ。
なんて言ってくれると思います。そこで、大切なのはとぼけること。
たまたまそうなったんだね
ぼくが子どもたちと算数をしていてよく使う言葉の1つが、
Tへぇよかったねぇ。たまたまそうなる数を選んだんだね。
と聞くことです。
子供たちが何か発見したときに「他の時も調べてみたい」という気持ちを引き出すためにはこの「たまたまじゃない?」という言葉はとっても有効です。子供たちは
Cたまたまじゃないよ!
Cだって、〇〇くんもなってるもん。
C違う数でもなってるよ。
と反論してくるはずです。でも中には、計算ミスでそうはなっていない子もいます。
Tでも、同じ数が続いてない人もいるよ。やっぱりたまたまなんじゃない?
ともう一度、子どもたちに問いかけます。すると、
C絶対ちがう!
C他の数でも試してみようよ!
と言い出します。
このように、自分たちから「他の数でもやってみたい」がひきだせたらしめたもの。もう子供たちは計算練習だということをわすれています。
他の数でもやってみよう おすすめ:誕生日
さて、他の数でやってみます。例えば誕生日などでも面白いですね。
7月12日:712
12月27日:1227
9月8日:98
というような形です。
やってみると、また教室がざわつき始めます。しかし今度は子どもたちから出ている空気が人によって違います。
Tどう?やっぱりたまたまだった?
Cううん。やっぱりできたよ。712だと712.712になった!
Cえ?できなかったよ。1227だと1228.227になっちゃった。
C98だとちょっと違うけど面白いよ。98.098になった!
と子どもたちから発表されるはずです。
ここで子どもたちに育てたい力は色々なパターンを出させて整理し、共通点を見出す力です。
Cできた数とできなかった数を整理しようよ!
という声を引き出したいですね。
みんなで数を出し合うと、
T3けたの時は同じ数が続いて、2けた、4けたは続かないんだね。
と具体例から決まりを発見することができるはずです。
子どもたちにこのパターンをいくつも出し、整理し共通点を見出す力がある程度育っていれば授業は自走していくでしょう。もしそだっていなければ今後の授業への種まきだととらえ、そのようなことをした子がいたら価値づけていきましょう。
なんでこうなるのかなぁ
さて、この部分は授業でふれてもいいですし自主学習にして個人で探求をさせるのもよいですね。
種明かしは簡単です。
①すきな3桁の数:□
②□×1.1=A
③A×7=B
④B×0.13=C
これを1つの式にすると、□×1.1×7×0.13となりますね。結合法則を使って式を変形すると
□×1.1×7×0.13=□×1.001となるわけです。そして、
□×1.001=□×1+□×0.001式変形できるので3桁の数が続くわけですね。
〇桁でもできないかなぁ
問いを広げる子を育てたいですね。
C2桁の数でやるにはどうすればいいかな。
Cもし4桁だったら?
と桁を変えて試してみようとする子がいたら本気でほめて価値づけましょう。
余談ですが…この実践は4年生でもできます
この問題、実は4年生でもできます。4年生で行うには
①好きな3けたの数:□
②□×11
③□×7
④□×13
のように、②③④でかける数を整数にすればよいわけです。
おわりに
今回も長くなってしまいました。
いかがだったでしょうか。ただの計算練習では子どもたちはなかなか笑顔にはなりません。
しかし、この授業のように計算練習をするといつの間にか何問も計算練習をすることになります。
毎回このような習熟の時間をとれるわけではありませんが何回かに1回はこのような時間が持てるときっと子どもたちの「笑顔」をつくることができるのではないでしょうか。



コメント